Body Double: Understanding the Astrophysics of a Newly-Discovered Multi-Planet Binary Star System

A look at Kepler 47 and the mathematical models that describe it

By Evelyn Lamb

DOUBLE FEATURE: An artist's depiction of the Kepler 47 system. Image: NASA/JPL-Caltech/T. Pyle

Last month astronomers announced the first discovery of multiple planets orbiting a pair of stars. Binary star systems, which comprise two stars orbiting around a common point, are very common?about half of sun-size stars are thought to be members of binary star systems. But it was only in 2011 that astronomers reported the first confirmed instance of a binary system with even a single planet. The newly discovered system, named Kepler 47, consists of a star about the size of the sun and a smaller companion, orbited by two planets.

The reason it has taken so long to find exoplanets around binary stars isn't because they are rare, but because it is hard for us to see them from an earthly vantage point. The data for the Kepler 47 discovery come from the Kepler space telescope, which orbits the sun, not Earth, so our planet doesn't block its view. The spacecraft's mission is to search for planets in the habitable zones around their suns, hopefully giving scientists a better idea of how many systems have planets that could support life.

Kepler detects exoplanets by measuring the tiny changes in a star's brightness caused by the passage of a body in front of it, ? la the?transit of Venus last witnessed in June. Thus, Kepler can only find planets whose orbits line up with its line of sight. Otherwise the planet will not alter the star's light from the telescope's point of view. Scientists thereby are limited in how many of these systems they can find; distant stars don't arrange themselves to provide a better view. Daniel Fabrycky, an astrophysicist at University of California, Santa Cruz, and one of the authors of the?paper announcing the discovery, says, "the punch line is that there's nothing special about it; planets can form around binary stars, too."

Any description of celestial motion starts with classical physics?specifically, Newton's law of gravitation. This law describes the force exerted on one body by another. It says that the force is proportional to the masses of the bodies and inversely proportional to the square of the distance between them. Because force equals mass times acceleration, one can use these two different descriptions of force to write a system of differential equations that will describe the motions of any number of bodies. The problem of describing their motion is called the n-body problem, where n represents the number of bodies in a system. It is actually not too hard to derive the equations, once given the masses and velocities of a bunch of bodies. But only the 2-body problem yields an explicit answer. The solutions for other values of n have to be found through numerical methods, which lead to arbitrarily accurate approximations, rather than by finding universal solutions to the equations.

A binary star system with two orbiting planets is a 4-body problem. But, Fabrycky says, in the case of Kepler-47 the two planets are so much smaller than the two suns that their masses can be assumed to be zero. Thus, the 4-body problem becomes a 2-body one for the two stars, because the planets don't tug on them very much. The solution to this 2-body problem is for each star to be in an elliptical orbit around the two bodies' center of mass. These orbits are described as Keplerian because Johannes Kepler?the Renaissance astronomer for whom the spacecraft is named?first noticed that the planets in our solar system have elliptical, not circular, orbits.

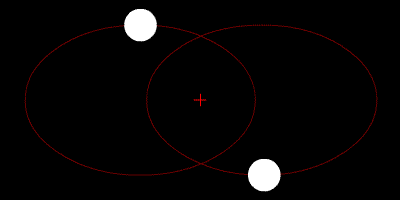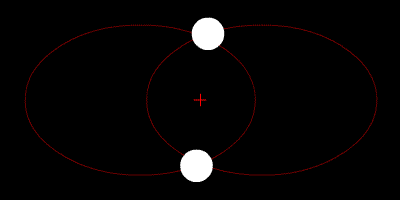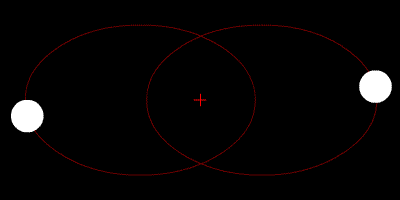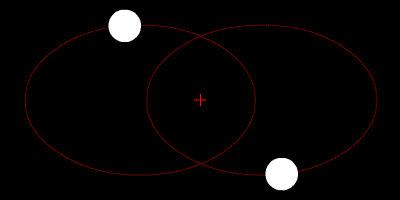
(At left, a simulation of two similarly sized stars in elliptical orbit around their center of mass, the red cross. Source: Wikimedia Commons/Zhatt)

Source: http://rss.sciam.com/click.phdo?i=e0662e52eb611d7ee9a1fbdc360d4b62

what time is the super bowl 2012 nfl mvp lana del rey snl performance nick diaz sheryl sandberg superbowl recipes super bowl kick off